10. Pharmacokinetics: zero and first order elimination kinetics, elimination half-life, volume of distribution, clearance, maintenance dose, loading dose, oral bioavailability

Page created on January 8, 2019. Last updated on January 7, 2022 at 21:53

Summary:

• If a drug follows first order elimination the rate of its elimination depends on the plasma concentration of the drug
  • This is because the mechanisms which eliminate the drug are not saturated
  • Almost all drugs follow first order kinetics
• If a drug follows zero order elimination the rate of its elimination is constant
  • This is because the mechanisms which eliminate the drug are saturated
  • Ethanol and salicylates follow zero order kinetics
  • Ethanol follows zero order kinetics because the cofactor for ADH, NAD⁺, is quickly depleted. The elimination of ethanol depends only on how fast the liver can regenerate NAD⁺ from NADH, which occurs at a constant rate
  • Phenytoin follows so-called non-linear pharmacokinetics, meaning that it follows zero order kinetics when given in high doses and first order kinetics when given in low doses
• The half-life of a drug is the time it takes for the plasma concentration of the drug to be reduced by 50%
• Knowing the half-life of a drug is useful for the following reasons:
  • It indicates how long it will take before the drug is completely eliminated from the body
  • It’s related to the duration of action of the drug
  • It’s related to the time needed to reach the steady state
  • It influences the size of fluctuation of the plasma concentration around the steady state concentration
• After 4 – 5 half-lives the drug is practically eliminated from the body
• Doubling the dose given of a drug increases the duration of action by one half-life
• Total body clearance is the sum of the clearance of the kidney, liver and other organs
• The steady state refers to a state where the concentration of a drug in the plasma is relatively constant
  • The dose rate is the amount of drug which needs to be administered every unit of time to achieve steady state
  • The dose rate depends on the total body clearence
  • Without a loading dose the steady state is reached after 4 – 5 half-lives
  • A loading dose is an initial large dose of drug which is given to immediately reach steady state
  • The size of the loading dose depends on the volume of distribution, the steady state concentration and the oral bioavailability
  • Maintenance doses are much smaller drug doses which are given after the loading dose to maintain the steady state

This topic is math-heavy. Also, some of the concepts mentioned in the title have been mentioned in other topics, including volume of distribution, clearance and oral bioavailability. 

This topic deals with quantitative pharmacokinetics, which deals with the mathematical description of absorption, distribution and elimination of drugs. We focus here mostly on the elimination of the drug, as that’s the most useful for a clinician.

The essence of the topic build around this: Drug elimination from the plasma may follow one of the two types of elimination:

1. The rate of elimination depends on the plasma concentration of the drug (first order elimination)
2. The rate of elimination is independent from the plasma concentration of the drug (zero order elimination)

First order elimination

First order elimination means simply that the drug is eliminated from the body faster if the plasma concentration is high than if the plasma concentration is low. Most drugs follow this pattern. This means that, if we plot a graph of the plasma concentration of a drug will the concentration fall faster just after administration of the drug. Let’s see what that looks like.

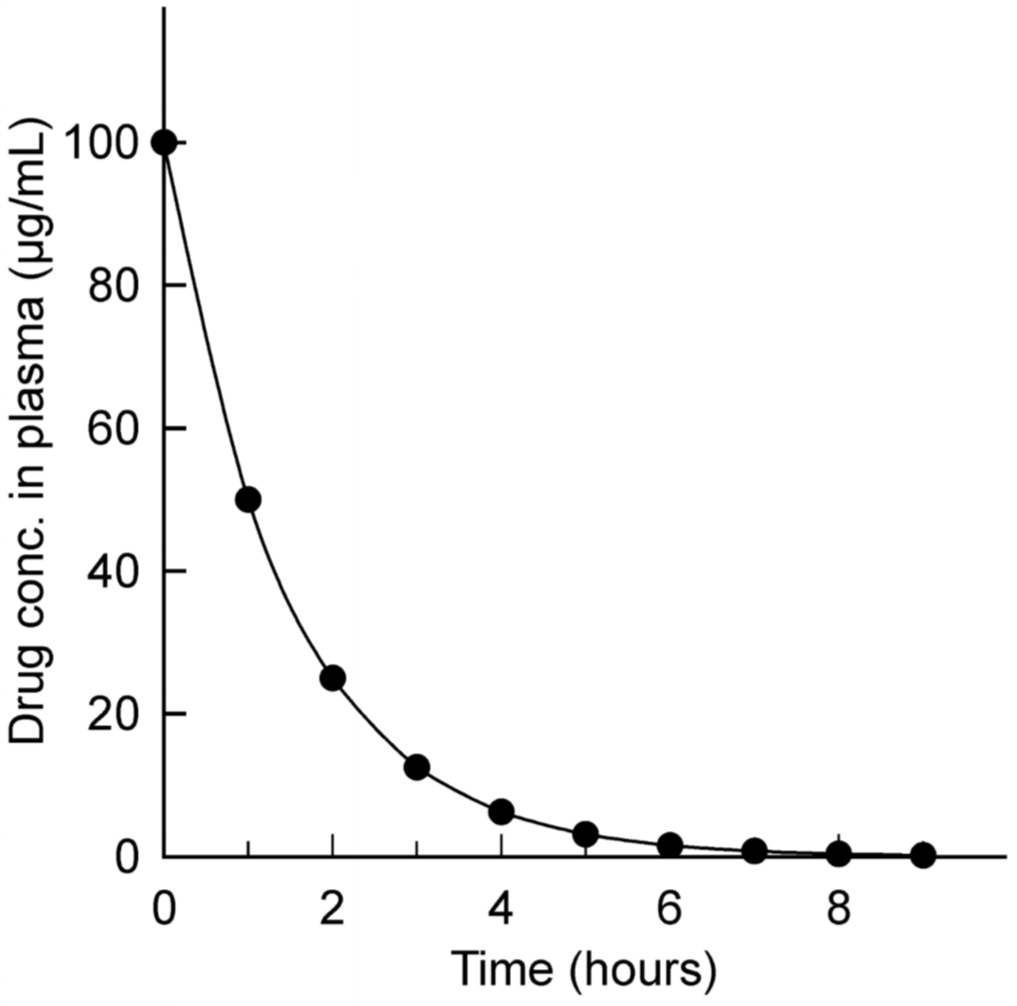
First-order elimination with arithmetic y-axis. The drug here was given intravenously at 0 hours.

Like we said – when drug concentration is high is the slope of the graph steep, meaning that elimination is faster. As the drug concentration decreases does the slope become lees steep, meaning that elimination slows down.

From hour 0 to hour 1 did the concentration fall from 100 to 50 µg/mL. That’s a decrease of 50µg/mL in one hour.

From hour 1 to hour 2 did the concentration fall from 50 to 25 µg/mL. That’s a decrease of 25 µg/mL in one hour.

We can see that the elimination rate decreases from hour to hour, but the fractional decline is constant. This just means that from hour to hour is the concentration decreased by the same fraction – in this case 1/2, or 50%. At hour 1 is the concentration 50% of what it was at hour 0. At hour 2 is the concentration 50% of what it was at hour 1 and so on.

This fractional decline has a name and constant – it’s called the elimination rate constant, K_el. In this case is K_el = 0.5/hour.

Zero order elimination

Zero order elimination means that the drug is eliminated from the body at the same rate no matter what the plasma concentration is. Let’s see what that looks like.

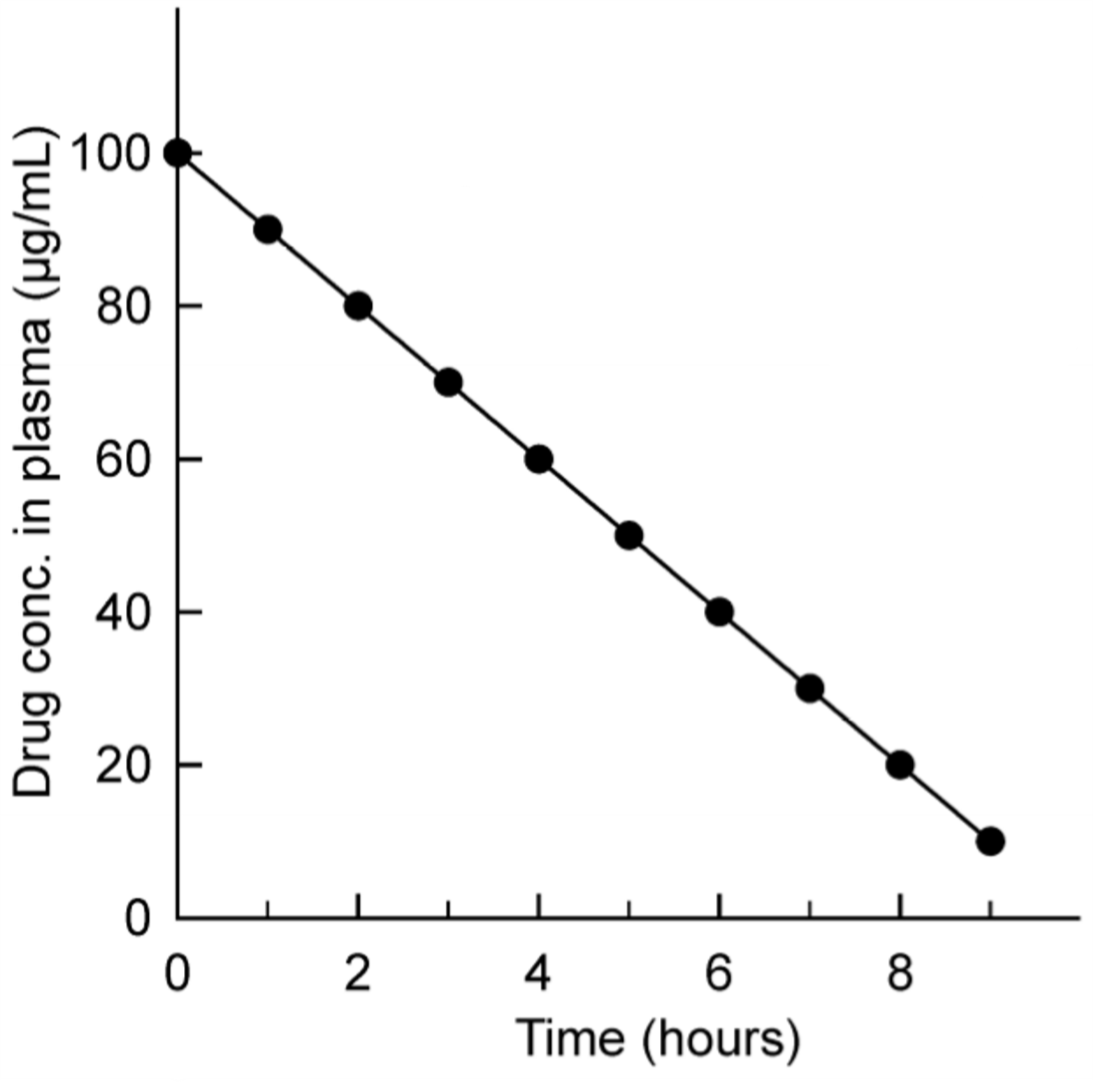
Zero-order kinetics with arithmetic y-axis.

Here can we see that the rate of elimination is constant. Every hour does the plasma concentration go down by 10 µg/mL.

The fractional decline in plasma concentration however is not constant. In the first hour does the plasma concentration go down from 100 to 90 µg/mL, which is a 10% reduction. In the second hour does it decrease from 90 to 80 µg/mL, which is an 11% reduction. In the third hour from 80 to 70 is there a 12.5% decrease. When the plasma concentration decreases, increases the fractional decline.

What determines the elimination kinetics?

We learned in previous topics that both diffusion and filtration are concentration-dependent processes. When the plasma concentration is higher will diffusion and filtration both go faster.

Enzymatic conversion and carrier-mediated transport by proteins are different. Enzymes and proteins have a maximum capacity they can work at, they can become saturated.

Let’s say we have a drug in the body. The liver has enzymes that convert this drug (purple) to an inactive metabolite (light blue), but the enzymes only have the capacity to convert 5 drug molecules every second.

There are only 5 enzymes, and each enzyme can only convert 1 molecule every second. Diffusion from the hepatic sinusoid into the hepatocyte is concentration-dependent. The higher the concentration of drug in the sinusoid, the faster the rate of diffusion. Let’s say the concentration is high, so 50 drug molecules diffuse into the hepatocyte every second. However, the enzymes can only convert 5 molecules per second, so it doesn’t matter what the concentration of the drug is – the drug molecules must just wait for the enzymes. The enzymes are a “bottleneck” in this system.

This system would show zero-order elimination. The rate of elimination would be constant – it’s equal to the rate of elimination of the “slowest” protein in the system, which in this case are the enzymes. The same principle works for transporter proteins.

Zero order elimination occurs only in systems where a protein, be it a biotransformation enzyme or a transport protein, which is involved in the elimination of the drug is saturated.

Drugs that are eliminated without the use of any protein, i.e. only by diffusion and/or filtration, can never show zero order elimination because their elimination isn’t dependant on any proteins.

In theory can any drug that is eliminated by a protein show zero order kinetics, as long as the concentration of the drug is so high that it saturates the protein. However, proteins and enzymes have high capacity. For many drugs is the concentration it would need to be in to show zero order elimination far higher than the therapeutic dose, so we will never see it.

One example of when we actually will see it is phenytoin. When phenytoin is given in doses less than 300 mg per day the CYP enzymes which biotransform it are not saturated, and so the elimination of phenytoin follows first-order kinetics. However, when it is given in doses larger than 300 mg per day the CYP enzymes are saturated, causing the elimination to switch to zero-order kinetics. These dose-dependent elimination kinetics are called non-linear or mixed-order pharmacokinetics.

Ethanol is a drug that shows zero order elimination at normally seen concentrations. Ethanol is metabolized by alcohol dehydrogenase, which needs NAD⁺ as a cofactor. The liver quickly runs out of NAD⁺, so alcohol dehydrogenase can only work as fast as the liver can reoxidise NADH back to NAD⁺. This means that the blood ethanol level is constant no matter what the blood concentration of it actually is. The rate of elimination is around 0.15 – 0.20 g/L every hour for adult men. Because the elimination is constant it be extrapolated backwards in time to determine what your blood alcohol concentration was some hours ago, keep that in mind.

Analysis of first order elimination

We will now analyse first order elimination in a special model called the one compartment model. It’s a very simplified model that doesn’t perfectly capture how things occur in the body. The body has multiple fluid compartments (plasma, interstitium, intracellular fluid).

We visualise the one compartment model as if the body was one single large fluid compartment. When a drug is injected IV into this one compartment body will the bod instantly distribute in the whole fluid compartment. The drug is also eliminated from this one compartment.

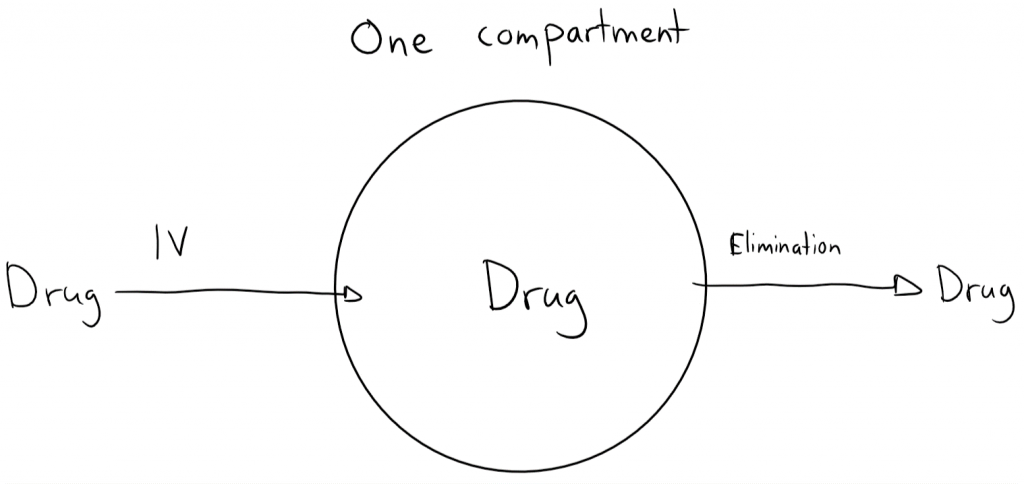
Let’s give a dose of a drug into this one compartment. The drug is D_IV, D for dose and IV for intravenous. At this point in time has no drug been eliminated yet, so the whole dose of drug is now inside the one compartment. The drug is instantly distributed in the whole compartment. We take a blood sample and find the concentration of the drug in the compartment, which we call C₀. C for concentration, 0 because we took the measurement after 0 seconds.

We can now use the old concentration = mass/volume equation to calculate the volume of the compartment. This volume is also known as the volume of distribution, V_d. The formula gives V_d = D_IV / C₀. That’s how we can calculate V_d for drugs.

As we’ve seen before the size of V_d indicates in which fluid spaces the drug usually distributes into. It’s important to know the V_d of drugs for two things:

1. The larger the V_d, the slower the rate of elimination
2. It’s essential to know V_d to calculate the loading dose, which we’ll look at later

We must introduce another symbol – T_1/2, which is the elimination half-life or simply half-life. The half life is the time it takes for the plasma concentration of a drug to decrease by 50%. T_1/2 can be calculated by the following formula: T_1/2 = 0.693 / K_el. K_el is the elimination rate constant, from earlier in this topic.

Because drugs which follow zero-order kinetics don’t have a constant fractional decline in plasma concentration they don’t have a true T_1/2 either.

Let’s look at why the half-life is important. There are four reasons:

1. It indicates how much time it will take before the drug is completely eliminated from the body
2. It’s related to the duration of action of the drug
3. It’s related to the time needed to reach the steady state (we’ll come back to this later)
4. It influences the size of fluctuation of the plasma concentration around the steady state concentration (also later)

Time passed after drug administration	Dose remaining in the body (%)	Dose eliminated from the body (%)
0 x T1/2	100	0
1 x T1/2	50	50
2 x T1/2	25	75
3 x T1/2	12.5	87.5
4 x T1/2	6.25	93.75
5 x T1/2	3.125	96.875

1: We can see that the drug is essentially gone from the body after 4 or 5 half-lives have passed. If we know the half-life of a drug can we easily estimate how long it will take for it to be completely eliminated, which is around 4 – 5 half-lives after administration.

2: Let’s say we give a general anaesthetic intravenously in two different doses. The patient wakes up when there is less than 12.5 mg of the drug in the body. We first give 100 mg of the drug. The half-life of the drug is 10 minutes.

Time passed after drug administration	Dose remaining in the body
0 x T1/2	100% – 100 mg
1 x T1/2	50% – 50 mg
2 x T1/2	25% – 25 mg
3 x T1/2	12.5% – 12.5 mg

The patient will wake up after 30 minutes. Now, let’s see what happens when we give a double dose, 200 mg.

Time passed after drug administration	Dose remaining in the body
0 x T1/2	100% – 200 mg
1 x T1/2	50% – 100 mg
2 x T1/2	25% – 50 mg
3 x T1/2	12.5% – 25 mg
4 x T1/2	6.25% – 12.5 mg

The patient will wake up after 40 minutes. So, doubling the dose increases the duration of action by just 1 half-life, 10 minutes!

Before we see reason 3 and 4 we must take some steps back and discuss steady state.

Steady state

Sometimes are we not interested in giving one dose of a drug. Sometimes we want to maintain a certain concentration of a drug in the blood of a patient over a period of time. This state is called the steady state. How often should the patient take the drug? How large should the doses of the drug be? This section will answer those questions.

We’ve talked about renal clearance, which is the volume of plasma that is cleared of the drug every minute. However, as we’ve seen isn’t the kidney the only organ that excretes drugs – the liver also contributes significantly.

The total body clearance (Cl) is the sum of the clearances of the different organs. In most cases is that just renal clearance and hepatic clearance, but in theory should we include pulmonary, glandular and gastrointestinal clearance as well: Cl = Cl_renal + Cl_hepatic + Cl_others

The total body clearance can be calculated if we give a drug intravenously in a certain concentration (D_IV) and monitor how its concentration changes with time. We make a graph that shows the plasma concentration over time and calculate the area under the curve (AUC). The total body clearance is the intravenous drug dose divided by this area: Cl = D_IV / AUC. Area under the curve has a unit of concentration x time, so for example mg/L/h or h x mg /L.

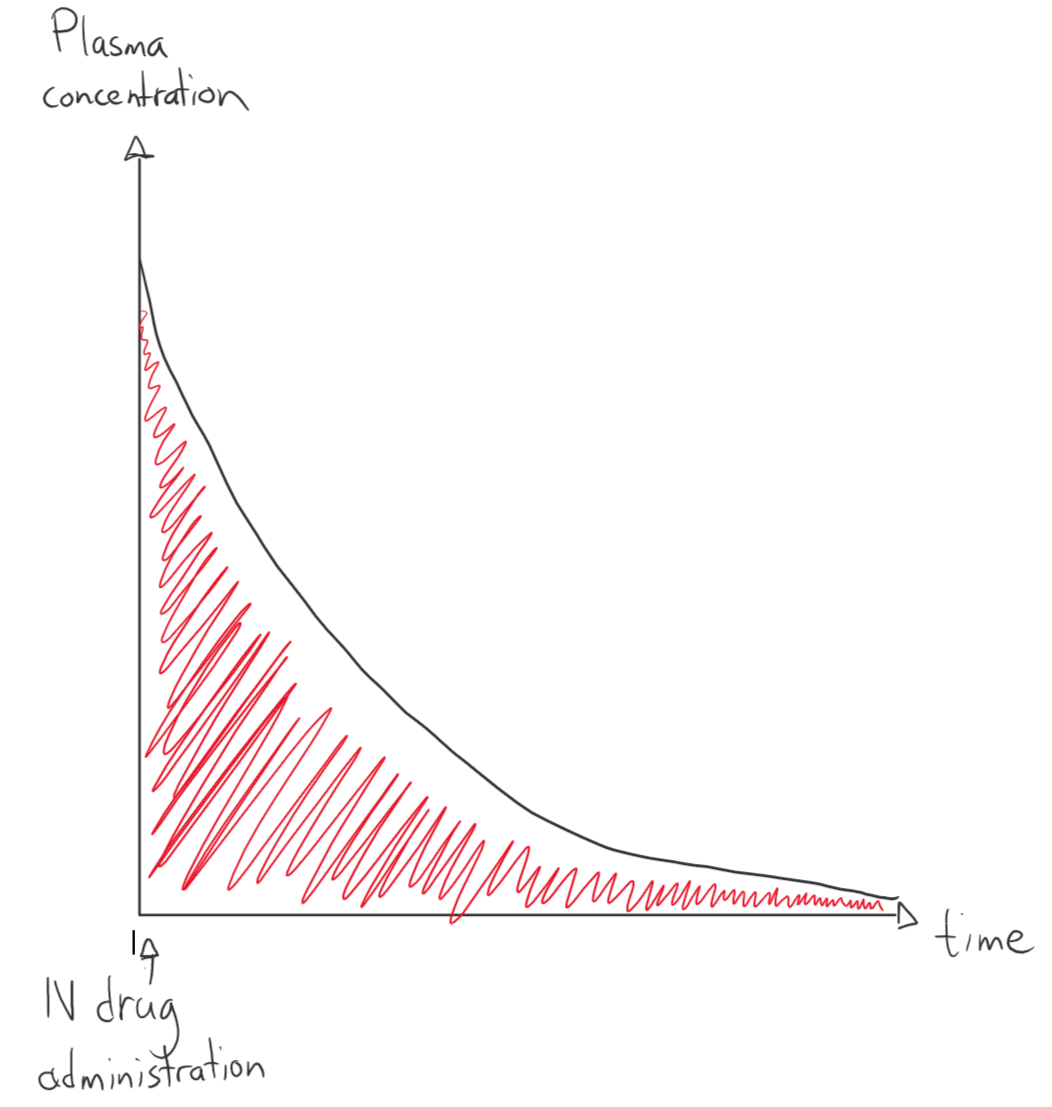
This graph shows how the plasma concentration changes with time after administration of a drug intravenously with first order elimination. The red area is the area under the curve.

Why is it important to know the total body clearance? It’s necessary to calculate the dose rate and the steady state concentration.

We want to maintain a certain concentration of drug in the blood, a steady state concentration (C_ss). If we know how quickly the body gets rid of the drug do we know how much drug we should administer to maintain the steady state concentration. The dose rate (DR) is the amount of drug that needs to be administered per unit of time. We calculate DR like this: DR = Cl x C_ss

For example, if we want to achieve a steady state concentration of 5 µg/mL of a certain drug, and that drug has a clearance of 50 mL/min will we have to give 50 mL/min x 5 µg/mL = 250 µg/min of the drug via continuous IV infusion.

However, when we want to give patient chronic treatments with drugs we rarely do that by giving them continuous intravenous infusion of the drug for the whole duration of the treatment. We rather tell them to take a certain dose of oral medication at multiple times every day. How do we achieve steady state then? To determine that must we first examine how the plasma concentration changes in oral drug administration. Up until now have we just looked at how things are with intravenous administration.

Pharmacokinetics of oral administration

When we give drugs intravenously is there no absorptive phase – the drug is instantly inserted into the plasma. When we give drugs orally however, there is a period of time where the drug is being absorbed into the body. While the plasma concentration increases as more and more of the drug is absorbed is the body already eliminating the drug that has already been absorbed. This makes the picture a little complicated. Let’s plot the plasma concentration over time as a curve.

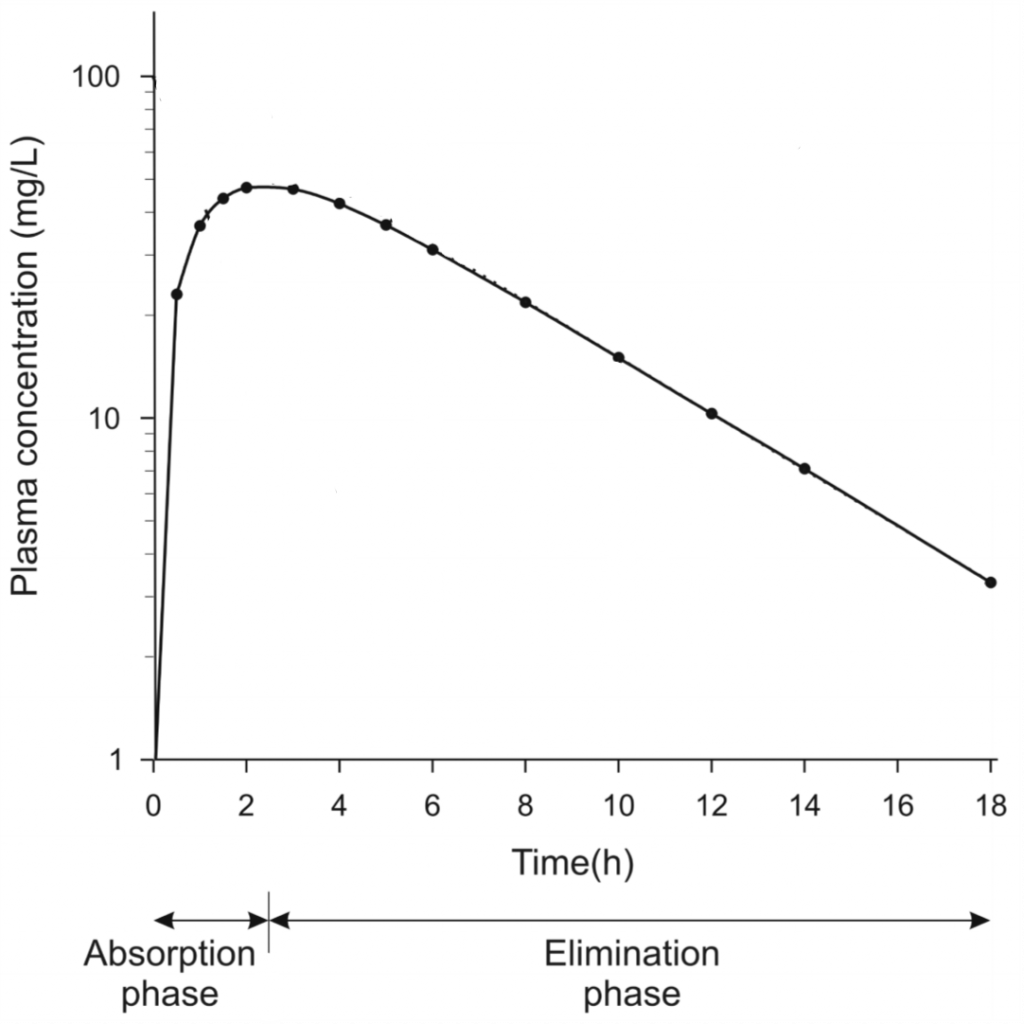
Plasma concentration over time after oral drug administration. Note that the y-axis is in logarithmic scale

We can see that the curve can be somewhat divided into the absorption phase, where the drug concentration increases because absorption occurs faster than elimination, and an elimination phase, where elimination is faster than absorption. Sometime during the elimination phase the drug is completely absorbed, meaning that only elimination occurs.

To calculate the total body clearance here must we account for oral bioavailability (F) as well. After all, in a previous topic we saw that whole oral dose (D_oral) doesn’t reach the systemic circulation because of the first pass effect. For oral drug administration is the clearance Cl = (F x D_oral)/AUC.

Now, what does the graph look like if we don’t just give the drug once, but multiple times? It depends on when we give the drug of course. If we give the second dose of the drug after the first has been completely eliminated will the graph just look like this:

Oral administration of two doses of a 400mg of a drug. The second dose was given after the first dose was already eliminated

The half-life of this drug is 6 hours, so it’s completely eliminated after approximately 4 half-lives, or 24 hours, as we can see on the graph.

Let’s say that this drug has a therapeutic window between 2 and 7 mg/L, as shown on the figure. If the plasma concentration of the drug is below 2 mg/L is the drug ineffective, and if it’s above 7 mg/L is it toxic. We can see from the figure that the patient has lower levels of the drug than 2 mg/L almost half of every day, and even a few hours where the drug levels are at toxic levels. That’s not good. What if we give smaller doses of the same drug, but more frequently?

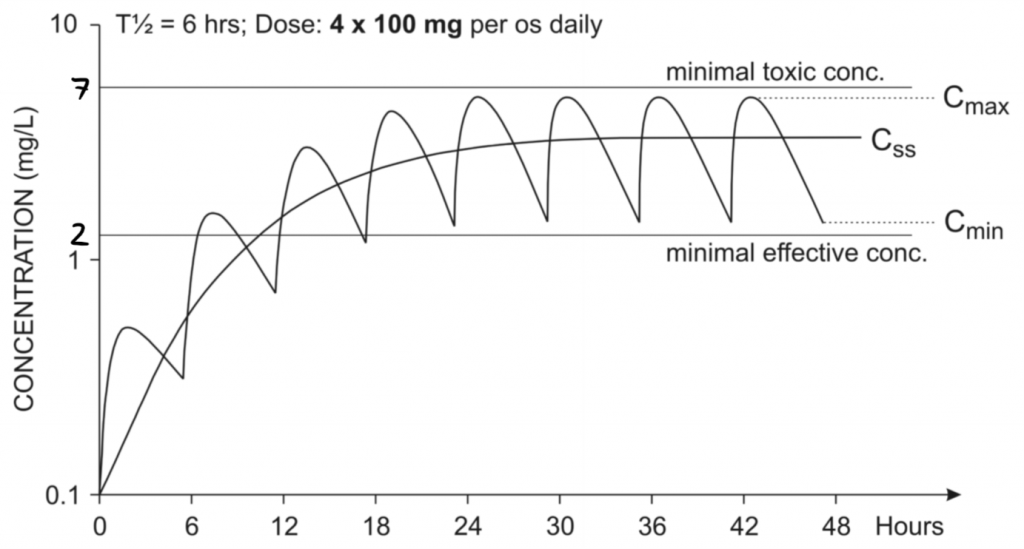
Oral administration of a multiple doses of 100 mg of a drug. The wavy line shows the actual drug concentration, while the C_ss line shows the average plasma concentration

This immediately looks much better. The drug concentration isn’t constant, but at least it’s always below toxic levels, and always above the minimal effective concentration after 12 hours of the first dose. This patient has reached steady state – he can keep taking 4 x 100 mg doses daily indefinitely and will never reach concentrations outside the therapeutic window.

The steady state concentration C_ss is the average of the maximal concentration C_max and the minimal concentration C_min.

The patient reached steady state after around 24 hours, which is again 4 half-lives. Steady state is always reached after 4-5 half-lives.

4-5 half-lives is a lot of time to wait in some cases. Digoxin for example is used to treat several heart conditions. It has a half-life of 2 days, meaning that steady state wouldn’t be reached until after 8 – 10 days! An even more crazy example is leflunomide, an anti-rheumatoid arthritis drug, which has 2 weeks half-life!

In certain cases it is beneficial for the patient to reach the therapeutic window as soon as possible, so we don’t have time to wait 4-5 half-lives. In these cases we can give a loading dose (D_L) – an initial large dose of the drug to “fill” the body up with the drug, and after that give maintenance doses that are much smaller than the loading dose but enough to maintain the steady state concentration.

The size of an intravenous loading dose is calculated like this: D_L = V_d x C_ss. For oral doses is it calculated like this: D_L = (V_d x C_ss) / F, where F is the oral availability.

Two-compartment model

All the previous findings work for the one-compartment model, however our body doesn’t have just one compartment. Another model, the two-compartment model assumes that the body has two compartments. However, I don’t think it’s important.